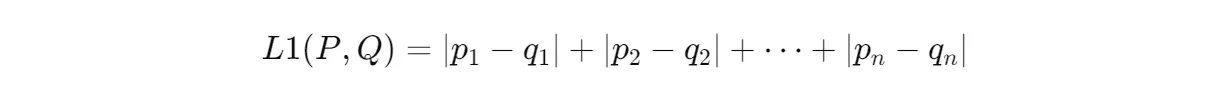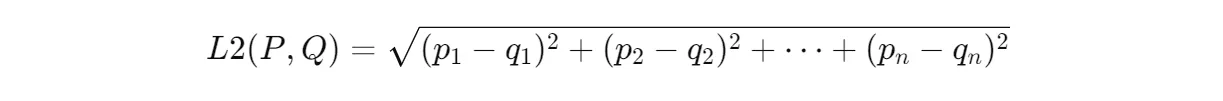How Does Vector Similarity Work
Summary by AI:
Vector similarity search converts data items into vectors in a high-dimensional space, with the distance between vectors indicating similarity. Techniques like Word Embeddings and Convolutional Neural Networks are used for text and non-text data respectively. Similarity is calculated using metrics like Euclidean Distance or Cosine Similarity, with Nearest Neighbor and Approximate Nearest Neighbor algorithms used for large datasets. Indexing structures and algorithms are used for efficient search. Applications of vector similarity search include recommendation systems, information retrieval, natural language processing, computer vision, bioinformatics, fraud detection, and customer support.
Vector Similarity Search works by converting data items (such as text documents, images, or audio clips) into vectors in a high-dimensional space. Each vector represents the features or characteristics of its corresponding item in a way that captures semantic or contextual meaning. The process of determining how "similar" two items are involves measuring the distance between their vectors in this space. Let's break down the key components and steps involved in vector similarity search:
1. Vector Representation
•
Text Data: Techniques like Word Embeddings (Word2Vec, GloVe), Sentence Embeddings (BERT, Sentence-BERT), or Document Embeddings are used to convert words, sentences, or entire documents into vectors. These embeddings capture semantic meaning, where similar words or sentences have vectors that are close to each other in the vector space.
•
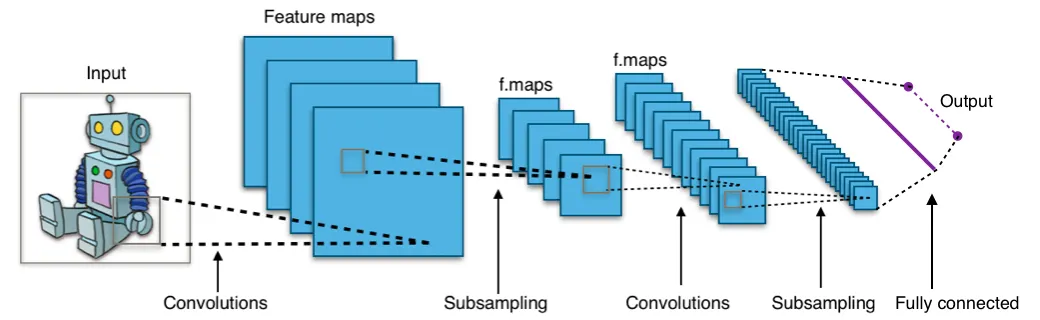
Non-Text Data: For images, audio, and other non-textual data, deep learning models (such as Convolutional Neural Networks for images) are used to extract features and encode them as vectors.
•
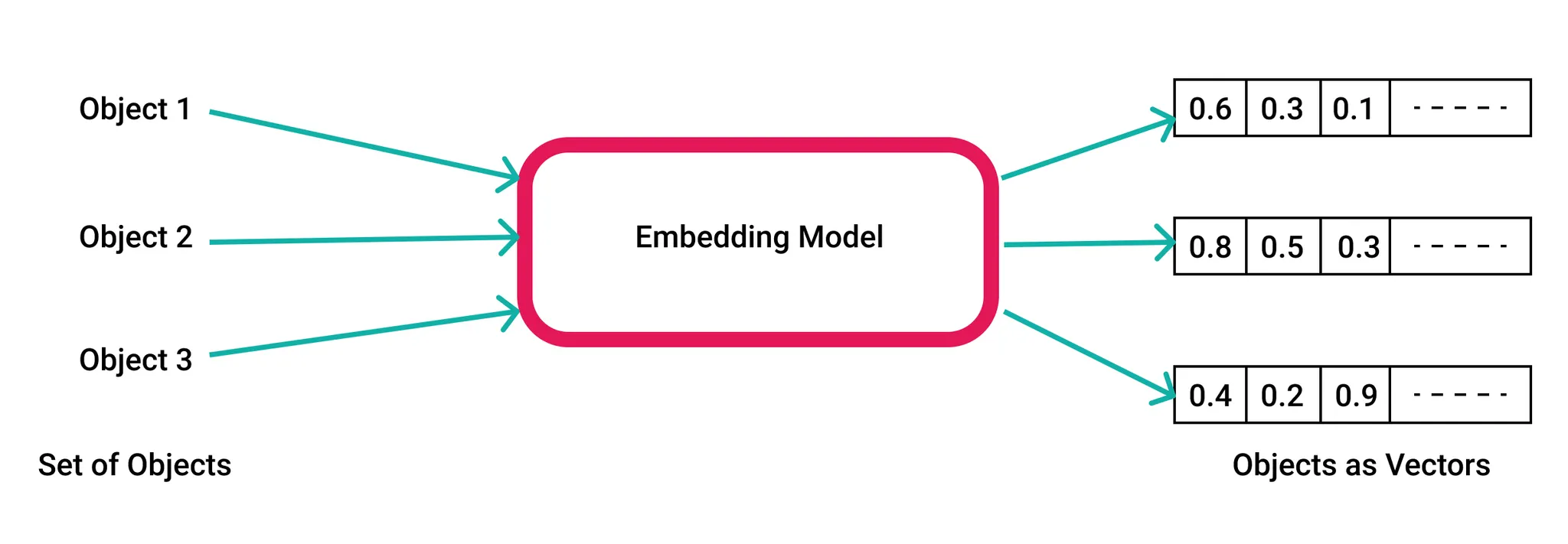
Vector Embedding
Vector Embedding Example
Vector embedding involves transforming high-dimensional data (like text, images, or sounds) into vectors of fixed size in a low-dimensional space.
Image Embedding Process in Computer Vision
Unlike raw data, which can be complex, unstructured, and challenging to work with directly, these vectors encapsulate the essential features and relationships of the data in a form that computers can efficiently process and analyze.
◦
Dimensionality Reduction: Embeddings convert data from high-dimensional (often sparse) spaces to lower-dimensional (dense) vector spaces. This process helps in revealing and preserving the intrinsic patterns, relationships, and structures within the data, despite the reduction in dimensions.
◦
Semantic Meaning: In the context of text data, embeddings are designed so that semantically similar words or phrases are mapped to points that are close to each other in the vector space. This property enables algorithms to understand and work with the meaning of words or sentences.
◦
Generalization: Embeddings capture the underlying essence of data items, allowing models to generalize better to unseen data by understanding its position and relation in the vector space.
2. Similarity Metrics
Once all items are represented as vectors, the similarity between them is calculated using distance or similarity metrics. The choice of metric can depend on the type of vectors and the specific requirements of the application. Common metrics include:
•
Basic Metrics
◦
Manhattan Distance(a.k.a. L1 Distance), Jaccard Similarity, and other metrics are also used based on the context and nature of the data.
◦
Euclidean Distance (a.k.a. L2 Distance) : The straight-line distance between two points in the vector space. It's intuitive but might not always capture the true semantic similarity for high-dimensional data.
◦
Cosine Similarity: Measures the cosine of the angle between two vectors, effectively capturing the orientation similarity regardless of magnitude. It's particularly popular for text data, as it can effectively measure directional closeness.
•
NN Algorithms:
NN Algorithms are used to find the most similar data points (neighbors) to a given query point within a dataset. The basic principle behind Nearest Neighbor algorithms is to compare the query point against all the points in the dataset to find the one(s) with the smallest distance or highest similarity.
◦
K-Nearest Neighbors (k-NN)
▪
k-NN is one of the simplest yet most effective and widely used algorithms. It identifies the 'k' closest points to the query point based on a distance metric (like Euclidean, Manhattan, or Cosine similarity) and makes decisions based on the majority label (for classification) or the average outcome (for regression) of these neighbors.
▪
The choice of 'k' is critical: too small a value makes the algorithm sensitive to noise, while too large a value makes it computationally expensive and possibly less accurate.
◦
Radius Neighbors
▪
Radius Neighbors considers all points within a fixed distance (radius) of the query point as its neighbors. This method is particularly useful when the density of the points varies significantly across the dataset.
▪
It helps in scenarios where the number of neighbors within a given radius can provide more insight than the k-nearest points, especially in unevenly distributed datasets.
•
Approximate Nearest Neighbor (ANN) Algorithms
Due to the computational complexity of exact nearest neighbor searches in large datasets, Approximate Nearest Neighbor (ANN) algorithms are often used. These algorithms aim to find the nearest neighbors quickly and with high probability, but without the guarantee of being exactly the nearest. They strike a balance between accuracy and computational efficiency.
◦
ANN Algorithms include:
▪
Locality-Sensitive Hashing (LSH): LSH hashes input items in such a way that similar items map to the same "buckets" with high probability. It reduces dimensionality and allows for faster searches at the cost of some accuracy.
▪
Tree-based Methods: Techniques like KD-trees and Ball Trees organize points in a tree structure based on their coordinates in the space, allowing for faster nearest neighbor searches by eliminating large portions of the search space.
▪
Graph-based Methods:
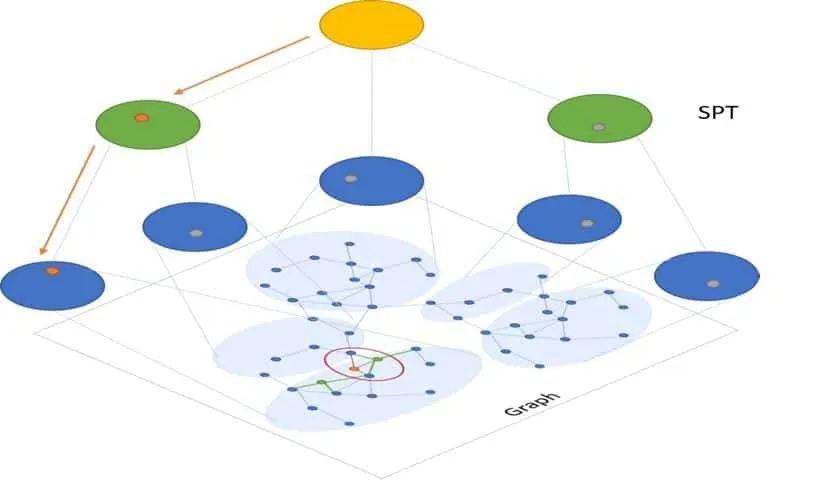
•
Space Partition Tree and Graph (SPTAG) :This algorithm assumes that the samples are represented as vectors and that the vectors can be compared by L2 distances or cosine distances. Vectors returned for a query vector are the vectors that have smallest L2 distance or cosine distances with the query vector
•
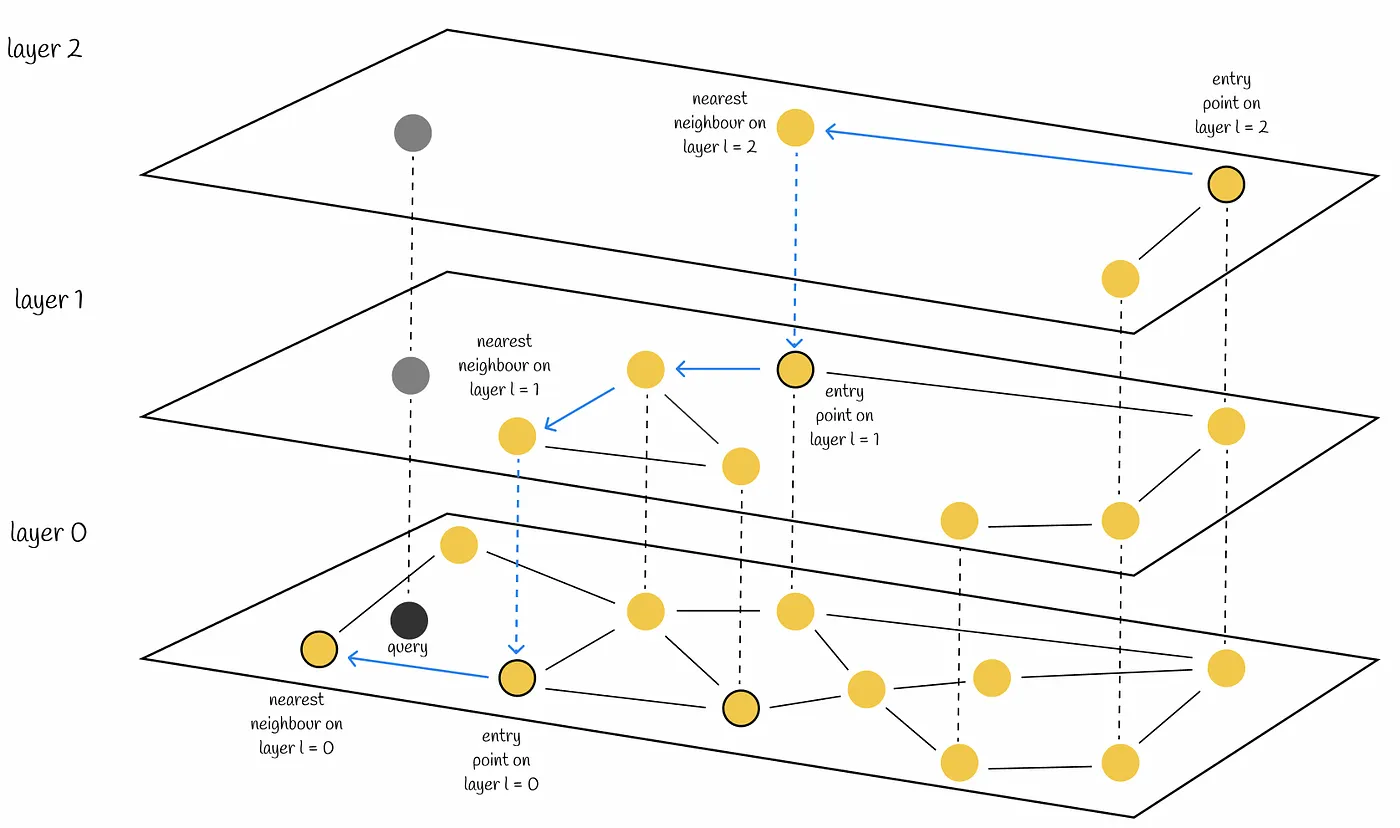
Hierarchical Navigable Small World (HNSW) construct a layered graph where each layer represents a different granularity of clustering. HNSW allows for efficient traversal of the graph to find nearest neighbors quickly.
◦
It uses a combination of randomization and local exploration to build a navigable graph structure.
▪
Vector Quantization: Methods like Product Quantization divide the space into a finite number of regions, each represented by a centroid. Data points are assigned to the nearest centroid, significantly reducing the search space for nearest neighbors.
3. Indexing and Search Algorithms
To efficiently search through millions or billions of vectors, vector similarity search systems use specialized indexing structures and algorithms. These are designed to speed up the retrieval of items that are most similar to a query vector, often through Approximate Nearest Neighbor (ANN) algorithms. Examples include:
•
Tree-based Indexes: Such as KD-trees and Ball-trees, which partition the vector space into regions.
•
Hashing-based Indexes: Like Locality-Sensitive Hashing (LSH), which buckets vectors so that similar items are more likely to be placed in the same bucket.
•
Graph-based Indexes: Such as Hierarchical Navigable Small World (HNSW) graphs, which create layers of connected graphs for efficient traversal.
•
Facebook’s Similarity Search Algorithm (FAISS)
◦
Faiss is a library developed by Facebook for efficient similarity search and clustering of dense vectors. It provides various indexing structures, such as inverted indices, product quantization, and IVFADC (Inverted File with Approximate Distance Calculation), which are optimized for different trade-offs between accuracy and speed.
Optimization Focus:
▪
Multi-threading to exploit multiple cores and perform parallel searches on multiple GPUs.
▪
BLAS libraries for efficient exact distance computations via matrix/matrix multiplication. An efficient brute-force implementation cannot be optimal without using BLAS. BLAS/LAPACK is the only mandatory software dependency of Faiss.
▪
Machine SIMD vectorization and popcount are used to speed up distance computations for isolated vectors.
4. Query Processing
When a query is received, it is first converted into a vector using the same process as the indexed items. The search algorithm then uses the chosen similarity metric to find the nearest vectors in the index, which correspond to the items most similar to the query.
Use cases for Vector Similarity Search
1. Recommendation Systems
•
E-commerce and Retail: Vector similarity search is used to recommend products to users based on the similarity of their past purchases or browsing history to available products. This can help increase sales by providing personalized recommendations.
•
Content Platforms: For video streaming, news, and music services, vector similarity search helps recommend content that matches a user's interests and past interactions, enhancing user engagement and satisfaction.
2. Information Retrieval
•
Semantic Search: In document retrieval systems, including web search engines, vector similarity search enables semantic search capabilities. It allows the system to find documents that are contextually related to the query, even if they don't share exact keywords, leading to more relevant search results.
•
Question Answering Systems: These systems use vector similarity search to find the most relevant pieces of information in response to a user's question, often by comparing the question vector to vectors of potential answers stored in a database.
3. Natural Language Processing (NLP)
•
Text Similarity and Clustering: Vector similarity search is used to group texts by topic or sentiment by measuring the similarity between document vectors. This is useful for applications such as news aggregation, sentiment analysis, and topic modeling.
•
Language Translation: By representing sentences or phrases as vectors, similarity search can help in finding matching phrases in different languages, aiding in machine translation systems.
4. Computer Vision
•
Image and Video Retrieval: Vector similarity search enables content-based image and video retrieval systems, where users can search for images or videos by providing an example image or specifying certain visual features.
•
Facial Recognition: In security and social media applications, facial recognition systems use vector similarity search to identify individuals by comparing the vector representation of their faces to a database of known faces.
5. Bioinformatics
•
Genomic Sequence Matching: Vector similarity search can be used to find similar genomic sequences, helping in the study of genetic diseases, evolutionary biology, and the development of gene therapies.
6. Fraud Detection and Anomaly Detection
•
Financial Services: Banks and financial institutions use vector similarity search to detect unusual patterns in transactions, helping to identify potential fraud by comparing transactions to known fraud vectors.
•
Network Security: In cybersecurity, anomaly detection systems identify potential threats by comparing network activity to vectors representing normal and abnormal behaviors.
7. Customer Support and Chatbots
•
Automated Customer Support: By converting customer queries and FAQs into vectors, similarity search can help chatbots and automated support systems provide relevant answers and support documentation to users.