Quick Sort (쾌속 정렬)
개요
쾌속 정렬 (Quick Sort)는 피벗 (Pivot) 을 선택하여 분할 정복으로 정렬하는 빠른 알고리즘으로, 메모리를 따로 사용하지 않는다는 장점이 있다. 시간 복잡도는 이나 최악의 경우 이 되기도 한다.
근데 분할-정복을 어디서 들어봤는데?
맞다. 바로 이전에 포스팅된 합병 정렬에서 다룬 내용이다.
합병 정렬과 퀵 정렬의 차이점은 순서라고 봐도 무방하다. 분할 후 정복하는 합병 정렬과 달리 정복 후 분할해나가는 퀵정렬이므로, 분할 과정과 정복 과정의 순서가 차이가 있다고 생각해도 무방해보이며, 퀵 정렬은 “Conquer and Divide” 알고리즘의 일부로도 불리곤 한다.
얼마나 빠르길래 “Quick”일까..?
퀵 정렬은 평균 시간 복잡도 O(n log n)을 가지고 있어, 대부분의 경우 매우 빠르게 작동한다. 특히 데이터가 무작위로 분포된 경우에 퀵 정렬은 그 성능을 극대화한다.
퀵 정렬은 대개 병합 정렬(Merge Sort)과 함께 효율적인 정렬 알고리즘으로 많이 비교된다. 병합 정렬과 달리 추가적인 메모리 공간을 거의 사용하지 않으며, 제자리(in-place)에서 정렬을 수행하므로, 메모리 효율이 매우 우수하다.
그러나, 최악의 경우 퀵 정렬의 성능은 가 된다. 이 경우는 피벗 선택이 항상 부적절하게 이루어져, 매번 한쪽으로만 데이터를 나누는 경우이다. 이를 방지하기 위해 피벗을 랜덤하게 선택하거나, 중간값을 피벗으로 설정하는 다양한 기법이 사용된다.
쾌속 정렬 작동 원리
퀵 정렬은 크게 두 가지 주요 단계로 작동한다.
1.
분할(Divide): 배열에서 하나의 요소를 피벗으로 선택한 뒤, 피벗보다 작은 값들은 왼쪽으로, 큰 값들은 오른쪽으로 이동시킨다.
2.
정복(Conquer): 피벗을 기준으로 나누어진 두 부분을 각각 재귀적으로 정렬한다.
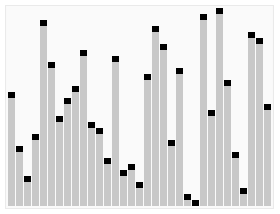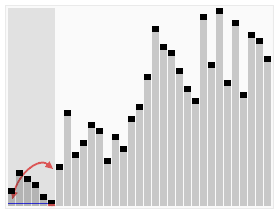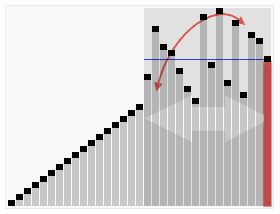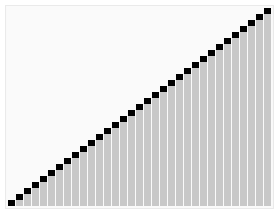
예를 들어, 배열 [9, 7, 5, 11, 12, 2, 14, 3, 10, 6]이 있다고 가정하자.
1.
피벗 선택: 배열의 첫 번째 요소를 피벗으로 선택한다. 여기서는 9를 피벗으로 선택한다.
2.
분할: 피벗 9를 기준으로 데이터를 나눈다. 피벗보다 작은 값들을 왼쪽으로, 큰 값들을 오른쪽으로 정렬한다.결과: [7, 5, 2, 3, 6, 9, 11, 12, 14, 10]
3.
재귀 호출: 피벗을 기준으로 나누어진 두 부분 [7, 5, 2, 3, 6]과 [11, 12, 14, 10]을 다시 재귀적으로 퀵 정렬을 수행한다.
4.
정렬 완료: 재귀 호출이 완료되면 전체 배열이 정렬된다.
이 과정을 반복하면서 배열 전체가 정렬된다.
위 설명은 정말 간략한 설명이고 자세한 과정은 아래에서 보자.
아래 수도 코드를 보며 다시 한 번 봐보자.
function 퀵정렬(배열, 시작, 끝):
if 시작 < 끝:
피벗인덱스 = 분할(배열, 시작, 끝)
퀵정렬(배열, 시작, 피벗인덱스 - 1) // 왼쪽 부분 정렬
퀵정렬(배열, 피벗인덱스 + 1, 끝) // 오른쪽 부분 정렬
function 분할(배열, 시작, 끝):
피벗 = 배열[시작]
왼쪽 = 시작 + 1
오른쪽 = 끝
while 왼쪽 <= 오른쪽:
while 왼쪽 <= 끝 그리고 배열[왼쪽] <= 피벗:
왼쪽 += 1
while 오른쪽 >= 시작 그리고 배열[오른쪽] > 피벗:
오른쪽 -= 1
if 왼쪽 < 오른쪽:
배열[왼쪽]과 배열[오른쪽]을 교환
배열[시작]과 배열[오른쪽]을 교환 // 피벗을 올바른 위치로 이동
return 오른쪽 // 피벗의 위치를 반환
C++
복사
•
1. 퀵정렬 함수
퀵 정렬 알고리즘의 핵심은 배열을 피벗(pivot)을 기준으로 두 부분으로 나누고, 각 부분을 재귀적으로 정렬하는 것이다. 이 과정은 퀵정렬 함수에서 수행된다.
function 퀵정렬(배열, 시작, 끝):
if 시작 < 끝:
피벗인덱스 = 분할(배열, 시작, 끝)
퀵정렬(배열, 시작, 피벗인덱스 - 1) // 왼쪽 부분 정렬
퀵정렬(배열, 피벗인덱스 + 1, 끝) // 오른쪽 부분 정렬
Plain Text
복사
1.
조건문(if 시작 < 끝): 배열의 시작 인덱스가 끝 인덱스보다 작을 때만 퀵 정렬을 수행한다. 이 조건은 재귀적으로 배열을 분할할 때, 배열이 더 이상 나눌 수 없을 만큼 작아졌을 경우 종료 조건으로 사용된다. 즉, 배열의 크기가 1 이하인 경우, 더 이상 정렬할 필요가 없으므로 재귀 호출을 중단한다.
2.
분할(배열, 시작, 끝) 호출: 분할 함수는 배열을 피벗을 기준으로 나누고, 피벗이 올바르게 정렬된 위치에 위치하도록 한다. 이때 분할 함수는 피벗이 위치한 인덱스를 반환하며, 이 인덱스를 기준으로 배열을 다시 좌우로 나누어 재귀적으로 정렬한다.
3.
재귀 호출:
•
왼쪽 부분(퀵정렬(배열, 시작, 피벗인덱스 - 1)): 피벗보다 작은 값을 가진 배열 부분을 정렬하기 위해 재귀적으로 호출한다.
•
오른쪽 부분(퀵정렬(배열, 피벗인덱스 + 1, 끝)): 피벗보다 큰 값을 가진 배열 부분을 정렬하기 위해 재귀적으로 호출한다.
•
2. 분할 함수 (파티션 함수)
분할 함수는 퀵 정렬의 핵심이다. 이 함수는 배열을 피벗을 기준으로 두 부분으로 나누고, 피벗을 올바른 위치에 배치하는 역할을 한다.
◦
파티션 함수는 임의의 피벗을 중심으로 그보다 작은 것은 왼쪽, 그보다 큰 것은 오른쪽으로 몰아 넣는 함수다.
function 분할(배열, 시작, 끝):
피벗 = 배열[시작]
왼쪽 = 시작 + 1
오른쪽 = 끝
while 왼쪽 <= 오른쪽:
while 왼쪽 <= 끝 그리고 배열[왼쪽] <= 피벗:
왼쪽 += 1
while 오른쪽 >= 시작 그리고 배열[오른쪽] > 피벗:
오른쪽 -= 1
if 왼쪽 < 오른쪽:
배열[왼쪽]과 배열[오른쪽]을 교환
배열[시작]과 배열[오른쪽]을 교환 // 피벗을 올바른 위치로 이동
return 오른쪽 // 피벗의 위치를 반환
Plain Text
복사
1.
피벗 선택(피벗 = 배열[시작]): 배열의 첫 번째 요소를 피벗으로 선택한다. 이 피벗은 나중에 배열의 올바른 위치로 이동하게 된다.
2.
두 인덱스 설정(왼쪽 = 시작 + 1, 오른쪽 = 끝): 왼쪽 인덱스는 피벗 다음 요소에서 시작하고, 오른쪽 인덱스는 배열의 끝에서 시작한다. 왼쪽은 피벗보다 큰 값을 찾고, 오른쪽은 피벗보다 작은 값을 찾는다.
3.
while 루프: 배열의 양쪽 끝에서부터 피벗을 기준으로 요소들을 비교하며, 피벗보다 작은 값과 큰 값을 교환한다.
•
첫 번째 while 왼쪽 <= 끝 그리고 배열[왼쪽] <= 피벗: 왼쪽 인덱스가 피벗보다 큰 값을 찾을 때까지 오른쪽으로 이동한다.
•
두 번째 while 오른쪽 >= 시작 그리고 배열[오른쪽] > 피벗: 오른쪽 인덱스가 피벗보다 작은 값을 찾을 때까지 왼쪽으로 이동한다.
4.
교환(if 왼쪽 < 오른쪽): 왼쪽 인덱스가 오른쪽 인덱스보다 작으면, 두 값을 교환하여 피벗을 기준으로 작은 값은 왼쪽으로, 큰 값은 오른쪽으로 이동시킨다.
5.
피벗의 위치 이동(배열[시작]과 배열[오른쪽]을 교환): 모든 교환이 끝난 후, 피벗을 오른쪽 인덱스에 위치한 값과 교환하여, 피벗을 배열의 올바른 위치에 배치한다.
6.
피벗의 인덱스 반환(return 오른쪽): 피벗이 위치한 인덱스를 반환한다. 이 인덱스를 기준으로 배열이 다시 좌우로 나누어지며, 재귀적으로 정렬이 진행된다.
예시로 과정을 다시 살펴보자.
퀵 정렬에서 피벗을 마지막 요소로 선정하는 기준으로, 배열 16, 4, 2, 38, 21, 5, 20, 27을 정렬하는 과정을 단계별로 설명한다.
예시로 다시 보는 퀵정렬
1. 첫 번째 호출: 배열 [16, 4, 2, 38, 21, 5, 20, 27]
2. 두 번째 호출: 배열 [16, 4, 2, 20, 21, 5]
3. 세 번째 호출: 배열 [2, 4] , [20, 21, 16]
4. 네 번째 호출
최종적으로 배열은 [2, 4, 5, 16, 20, 21, 27, 38]로 정렬된다.
전체 과정 요약
1.
배열을 피벗으로 분할하고, 피벗을 올바른 위치에 놓는다.
2.
피벗 기준으로 왼쪽과 오른쪽 부분을 재귀적으로 정렬한다.
3.
분할이 완료되면 최종 정렬된 배열이 완성된다.
만약에.. 아주 만약에…
피벗(Pivot)이 항상 최대값이면 어떨까? 사실 선택정렬과 다를바가 없어진다. 최대값만을 피벗으로 가지면 최대값을 선택하는 것과 다름이 없으니까 말이다. 이와 같이 퀵 정렬의 성능은 피벗 선택에 크게 의존한다. 피벗을 어떻게 선택하느냐에 따라 성능이 에서 까지 달라질 수 있다.
쾌속 정렬의 단점은 위에서 말한 피벗의 문제도 있으나, 비안정 정렬이라는 점이 추가적인 문제가 된다. 퀵 정렬은 비안정 정렬이다. 즉, 배열 내에 동일한 값이 여러 개 있을 때, 이 값들의 상대적인 순서가 변할 수 있다.
예를 들어, [3, 1, 3, 2]라는 배열에서 퀵 정렬을 수행하면, 3의 순서가 바뀔 수 있다. 이러한 성질 때문에 안정성이 필요한 상황에서는 퀵 정렬을 사용할 수 없다. 반면, 병합 정렬(Merge Sort) 같은 알고리즘은 안정성을 보장한다.
여러 가지 문제 상황을 정리해보자면,
퀵 정렬이 문제가 되는 상황들..
그러나, 쾌속 정렬은 유용하다!
바로 데이터를 따로 저장할 임시 공간이 필요 없다는 점이 장점으로 뽑힌다. 합병 정렬은 정렬이 되면서 계속 메모리 공간이 필요한 반면, 쾌속 정렬은 그런 메모리가 필요가 없다.
또한, 비안정 정렬임에도 빠르고 효율적이지 않은가! 이것만으로 해도 충분한 이유일 것이다.
컴퓨터 시스템 내부의 기본 정렬 방법인 시스템 정렬에는 주로 쾌속정렬이 사용된다고 한다 (주우석, 2015) 메디안 값(중앙 값)을 피벗으로 하여 최적화하기도 하고, 파티션이 어느 정도 작아지면 정렬을 끝내기도 한다.
나름 최악의 상황을 가지 않기 위한 최적화 방법들이 여럿 존재하는 것으로 보인다.
쾌속 정렬 코드 (C++)
#include <iostream>
using namespace std;
// 배열을 분할하고 피벗의 위치를 반환하는 함수
int partition(int arr[], int low, int high) {
int pivot = arr[low]; // 피벗을 첫 번째 요소로 설정
int left = low + 1;
int right = high;
while (left <= right) {
// 피벗보다 큰 요소를 찾을 때까지 왼쪽 이동
while (left <= high && arr[left] <= pivot) left++;
// 피벗보다 작은 요소를 찾을 때까지 오른쪽 이동
while (right >= low && arr[right] > pivot) right--;
if (left < right) {
swap(arr[left], arr[right]);
}
}
// 피벗을 올바른 위치에 놓기
swap(arr[low], arr[right]);
return right; // 피벗의 최종 위치 반환
}
// 퀵 정렬 함수
void quickSort(int arr[], int low, int high) {
if (low < high) {
int pivotIndex = partition(arr, low, high); // 분할
quickSort(arr, low, pivotIndex - 1); // 왼쪽 부분 정렬
quickSort(arr, pivotIndex + 1, high); // 오른쪽 부분 정렬
}
}
int main() {
int arr[] = {9, 7, 5, 11, 12, 2, 14, 3, 10, 6};
int n = sizeof(arr) / sizeof(arr[0]);
quickSort(arr, 0, n - 1);
// 정렬된 배열 출력
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
cout << endl;
return 0;
}
C++
복사
요약
1.
퀵 정렬은 평균적으로 O(n log n)의 빠른 성능을 가지지만, 피벗 선택이 부적절하면 최악의 경우 O(n^2)의 성능을 보일 수 있다.
2.
퀵 정렬은 비안정 정렬로, 동일한 값의 순서가 보장되지 않으며, 합병 정렬과 달리 추가 메모리 공간이 거의 필요하지 않다.
3.
피벗 선택에 따라 성능이 좌우되지만, 최적화 기법을 적용하면 퀵 정렬은 빠르고 메모리 효율이 높은 유용한 정렬 알고리즘이다.
REFERENCES
2.
주우석, 2015, C/C++로 배우는 자료구조론, 한빛미디어
Written by Changyu Lee