Dynamic Programming (동적 계획법, DP)
개요
동적 계획법(Dynamic Programming, DP)은 복잡한 문제를 해결하기 위해 작은 하위 문제로 나누고, 그 결과를 저장하여 동일한 하위 문제를 반복 계산하지 않는 방법이다. DP는 주로 최적화 문제에서 사용되며, 효율적인 알고리즘 설계를 위해 중요한 도구이다.
동적 계획법(DP)의 이해
•
DP란 무엇인가?
◦
동적 계획법(DP)의 핵심은 분할-정복과 같은 접근 방식으로 주어진 문제를 더 작은 문제로 분할하여 각 조각의 답을 계산하고 원래 문제에 대한 답을 계산해나가는 알고리즘 디자인 패러다임이다.
DP는 보통 알고리즘 대회나 문제풀이에서 메모리를 사용하여 복잡한 계산과정을 덜어내는 방식으로 사용된다.
이런 메모리들을 캐시 (Cache) 라고 부르며, 두 번 이상 계산되는 부분 문제를 ‘중복되는 부분 문제’ 라고 부른다.
동적 계획법이 사용되는 제일 유명한 예는 이항 계수이다.
위 점화식을 풀기 위해서 재귀 호출을 계속 하게 되는데, 계산을 하다보면 중복되는 연산을 계속하게 된다.
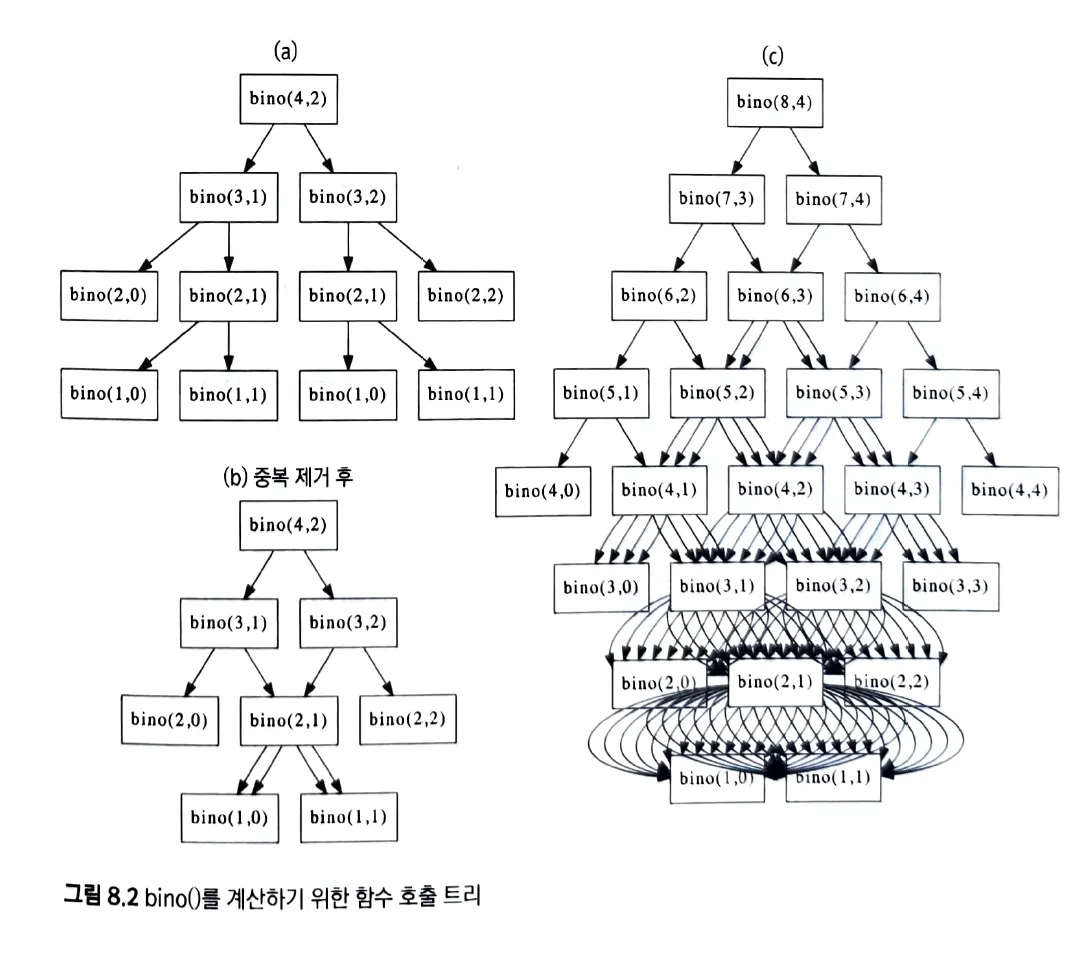
이항 계수를 계산하는 과정을 트리 형태로 나타내면 다음과 같다.
구종만, 2012, 프로그래밍 대회에서 배우는 알고리즘 문제해결전략 1, 인사이트
메모이제이션 vs 반복적 DP
•
메모이제이션 기법 (탑다운 방식)
이항계수를 계산하는 과정을 최적화시키는데 주목할 것은 에 따라 나오는 결과값이 항상 똑같다는 것이다.
이를 캐시 배열을 만들어서 이전에 계산했던 내용을 저장하면 계산과정을 최적화 시킬 수 있다.
이런 방식처럼, 함수의 결과를 저장하는 메모리를 사용하여 한 번 계산한 값을 저장해뒀다 재활용하는 최적화 기법을 메모이제이션 (Memoization) 기법이라고 한다.
이 기법을 활용하여 두 번 이상 반복 계산되는 부분 문제들의 답을 미리 저장하고 속도의 향상을 꾀하는 알고리즘 설계 기법을 DP라 하는 것이다.
메모이제이션의 시간 복잡도는 다음과 같은 식을 사용한다.
(존재하는 부분 문제의 수) x (한 부분 문제를 풀 때 필요한 반복문의 수행 횟수)
Python
복사
•
반복적 동적 계획법 (바텀업 방식)
문제를 가장 작은 하위 문제부터 시작해 점차 큰 문제를 해결하는 방식입니다. 반복문을 사용하여 재귀 호출을 피하고, 메모리 사용을 최적화하는 방법이다.
사실상 메모이제이션과 다를 바가 없다. 다만 연산이 굉장히 많은 상황에서 재귀 호출이 많아지면 스택 메모리가 가득차서 오버플로우가 날 수 있다.
•
반복적 동적 계획법과 재귀적 동적 계획법의 비교
비교 항목 | 반복적 동적 계획법 (바텀업) | 재귀적 동적 계획법 (탑다운) |
접근 방식 | 작은 하위 문제부터 시작해 점차 큰 문제를 해결함 | 큰 문제를 먼저 해결하고 작은 하위 문제로 재귀적으로 나눔 |
메모리 사용 | 문제 크기에 따라 일정한 메모리 사용 | 메모이제이션을 사용하여 중복 계산 방지, 재귀 호출로 추가 메모리 사용 가능 |
재귀 호출 | 없음 (반복문 사용) | 재귀 호출을 사용함 |
성능 | 재귀 호출 오버헤드가 없으므로 대체로 더 빠름 | 재귀 호출로 인한 오버헤드 발생 가능 |
코드 구조 | 간결하고 반복적인 코드 구조 | 재귀적으로 직관적인 구조이지만, 깊은 호출 스택이 필요할 수 있음 |
슬라이딩 윈도우 기법 | 사용 가능 | 불가능 |
추가적인 단점 | 부분 문제 간의 의존 관계를 고려해 계산되는 순서를 고민해야함 | 스택 오버플로우 위험성이 존재한다 |
◦
자세한 내용은 밑에서 설명하겠다.
DP를 활용한 프로그래밍 설계 방법론
1.
재귀 호출에서 시작하기
2.
메모이제이션 적용
이항 계수 DP 풀이 (C++)
#include <stdio.h>
#include <cstring>
int cache[30][30];
int bino(int n, int r) {
//기저
if(r ==0 || n ==r ) return 1;
if(cache[n][r] != -1) return cache[n][r];
return cache[n][r] = bino(n-1,r-1) + bino(n-1,r);
}
int main() {
memset(cache, -1, sizeof(cache)); // -1 == SENTINEL VAL
int res = bino(5,3);
printf("%d", res); // 10
}
C++
복사
피보나치 수열의 DP 적용 (Python)
일반적인 피보나치 수열을 구현한 것을 봐보자.
# 피보나치 수열 재귀 구현
def fibonacci(n):
if n <= 1:
return n
return fibonacci(n-1) + fibonacci(n-2)
Python
복사
방식은 간단하지만 일반 재귀적 해결법의 비효율성이 존재한다.
•
스택 오버플로우
재귀 깊이가 커지면 함수 호출 스택이 과도하게 쌓여 스택 오버플로우가 발생할 수 있다.
프로세스 메모리 구조에 대해 간단히 설명하자면, 프로세스는 주로 스택과 힙으로 메모리를 나누어 사용하며, 스택은 함수 호출 정보를 저장한다. 재귀가 깊어질수록 스택을 과도하게 사용하게 되어 문제가 생긴다.
•
재귀 호출로 인한 오버헤드 발생
동일한 하위 문제가 반복적으로 호출되면서, 불필요한 연산이 계속 발생한다. 예를 들어, fibonacci(5)를 계산할 때 fibonacci(3)가 두 번 계산되는 비효율이 발생한다.
이를 메모이제이션을 통해 최적화 해보자.
# 피보나치 수열 메모이제이션으로 구현
def fibonacci_memo(n, memo={}):
if n in memo:
return memo[n]
if n <= 1:
return n
memo[n] = fibonacci_memo(n-1, memo) + fibonacci_memo(n-2, memo)
return memo[n]
Python
복사
•
반복적 동적 계획법 방식을 통한 성능 개선
# 반복적 동적 계획법으로 구현
def fibonacci_dp(n):
if n <= 1:
return n
fib = [0] * (n+1)
fib[1] = 1
for i in range(2, n+1):
fib[i] = fib[i-1] + fib[i-2]
return fib[n]
Python
복사
최단 경로 문제와 DP
•
최단 경로 문제 또한 최적화 문제에 해당하므로, 이미 걸어온 경로에서 최적값을 저장해뒀다가 이를 꺼내서 다시 계산하는 방식으로 최적화시킬 수 있다. 그래서 최단 경로 문제도 DP를 사용하기도 한다.
최소 경로 문제의 DP 구현
# 최소 경로 문제 DP 구현 예시
def min_path_cost(grid):
rows, cols = len(grid), len(grid[0])
dp = [[0] * cols for _ in range(rows)]
dp[0][0] = grid[0][0]
for i in range(1, rows):
dp[i][0] = dp[i-1][0] + grid[i][0]
for j in range(1, cols):
dp[0][j] = dp[0][j] + grid[0][j]
for i in range(1, rows):
for j in range(1, cols):
dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]
return dp[-1][-1]
Python
복사
참고로,
1.
서울대 AI 대학원 2023년 후기 구술 면접에서 프로그래밍의 기초를 신청했을 때 나왔던 문제가 위 피보나치와 반복적 동적 계획법이다.
•
첫번째, 피보나치 수열 재귀 구현 빈칸 채우기
•
두번째, 재귀적 구현의 문제점
•
세번째, 피보나치 수열의 반복적 DP 활용한 구현 빈칸 채우기
지금 생각해보면 대체 왜 공부를 안했을까 싶다.
요약
•
DP는 복잡한 문제를 해결하기 위해 작은 하위 문제로 나누고, 그 결과를 저장하여 동일한 하위 문제를 반복 계산하지 않는 방법이다.
•
DP는 이항계수, 피보나치 수열 등이 있다.
•
DP에는 두 가지 방식이 존재한다. 메모이제이션과 반복적 DP.
•
DP는 아프다…(?)
REFERENCES
1.
구종만, 2012, 프로그래밍 대회에서 배우는 알고리즘 문제해결전략 1, 인사이트
Written by Changyu Lee