선택 정렬 (Selection Sort)
개요
지금부터 본격적인 기본 정렬 알고리즘을 공부해보자.
선택 정렬: 배열에서 가장 작은 값을 선택해 앞에서부터 순서대로 정렬하는 방식이며, 시간 복잡도는 O(n²)이다.
왜 “선택” 인가?
선택 정렬은 정렬 과정에서 하나를 고정하고, 바꿀 대상을 “선택”해서 바꾸는 알고리즘이다.
대부분 이야기하는 선택 정렬은 값이 큰 데이터를 맨 뒤로 보내는 것이 일반적으로 보이며, 오름차순으로 정렬을 하며 가장 큰 값을 찾고, 이를 정렬의 대상이 되는 마지막 데이터를 선택해서 바꾸는 알고리즘이다.
여기서는 반대로, 최소값을 앞으로 먼저 보내는 걸 생각을 하겠다. 0부터 시작하는 반복문을 짜므로 조금 더 편한 방식이라고 생각이 되기 때문이다.
# 수도 코드
선택정렬(배열 A, 길이 n)
for i = 0 to n-1
minIndex = i
for j = i+1 to n-1
if A[j] < A[minIndex]
minIndex = j
if minIndex != i
A[i]와 A[minIndex]를 교환
Python
복사
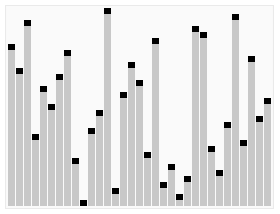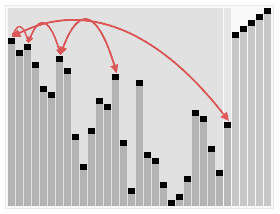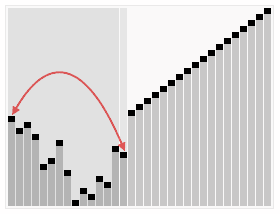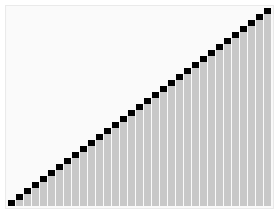
선택 정렬의 동작 과정
위 그래픽에서 필수적인 과정들이 다 나온다.
핵심은 가장 큰 값을 찾고, 맨 뒤로 보낸다는 것.
그래서 이중 반복문을 보통 쓴다.
큰 값을 먼저 찾고, 이를 맨 뒤로 배치하기 때문이다.
우리는 최소값을 먼저 앞으로 배치하는 걸 생각하기로 했으므로, 조금 더 살펴보면.
이중 반복문을 통해
1.
배열의 첫 번째 원소부터 탐색을 시작한다.
2.
현재 위치에서부터 배열의 끝까지 중 가장 작은 원소를 찾는다.
3.
그 가장 작은 원소와 현재 위치의 원소를 교환(swap)한다.
4.
다음 위치로 이동하여 1~3 과정을 반복한다.
위 동작 과정이 기본적인 동작 과정이라고 보면 된다.
따라서 선택 정렬은 의 시간 복잡도를 갖는다. 이중 반복문으로 전체를 순회하기 때문이다.
선택 정렬 알고리즘 코드 (C++)
•
최소값을 찾아서 바꾸는 방식을 사용하기로 한다.
#include <stdio.h>
// 데이터 입력
int arr[1000];
int main(){
// 입력 데이터 크기 n
int numbers = 0;
scanf("%d", &numbers);
// 데이터 입력
for (int i = 0; i < numbers; i++) {
scanf("%d", &arr[i]);
}
for (int i = 0; i < numbers-1; i++) {
int minima = arr[i];
int minima_index = i;
for (int k = i+1 ; k < numbers; k++) {
//최소값 찾기
if (minima > arr[k]) {
minima = arr[k];
minima_index = k;
}
}
// 요소 변경
arr[minima_index] = arr[i];
arr[i] = minima;
}
//출력
for (int i = 0; i < numbers; i++) {
printf("%d ", arr[i]);
}
}
C++
복사
추가적으로,
선택 정렬은 정렬을 어떻게 하는가, 또 언제 요소를 바꾸냐에 따라 다양한 코드가 나올 수 있다.
우선, 정렬을 제일 작은 값을 변경하는 것이 아니라, 제일 큰 값을 먼저 찾아서 진행할 수도 있다. 앞에서부터 찾아가면서 최대값을 맨 뒤에 보내면 되니까… 뭐 그리 어렵지는 않은 알고리즘이다.
문제 상황과 요구에 따라 요소를 바꾸는 시점도 달라질 수 있다. 뭐 그건 사실 정렬 알고리즘 문제들 전부 비슷한 상황이니까.. 결국은 케바케로 들어가야하지 않나 싶다.
REFERENCES
Written by Changyu Lee, 2024-10-12