Graph Algorithm (그래프 알고리즘)
개요
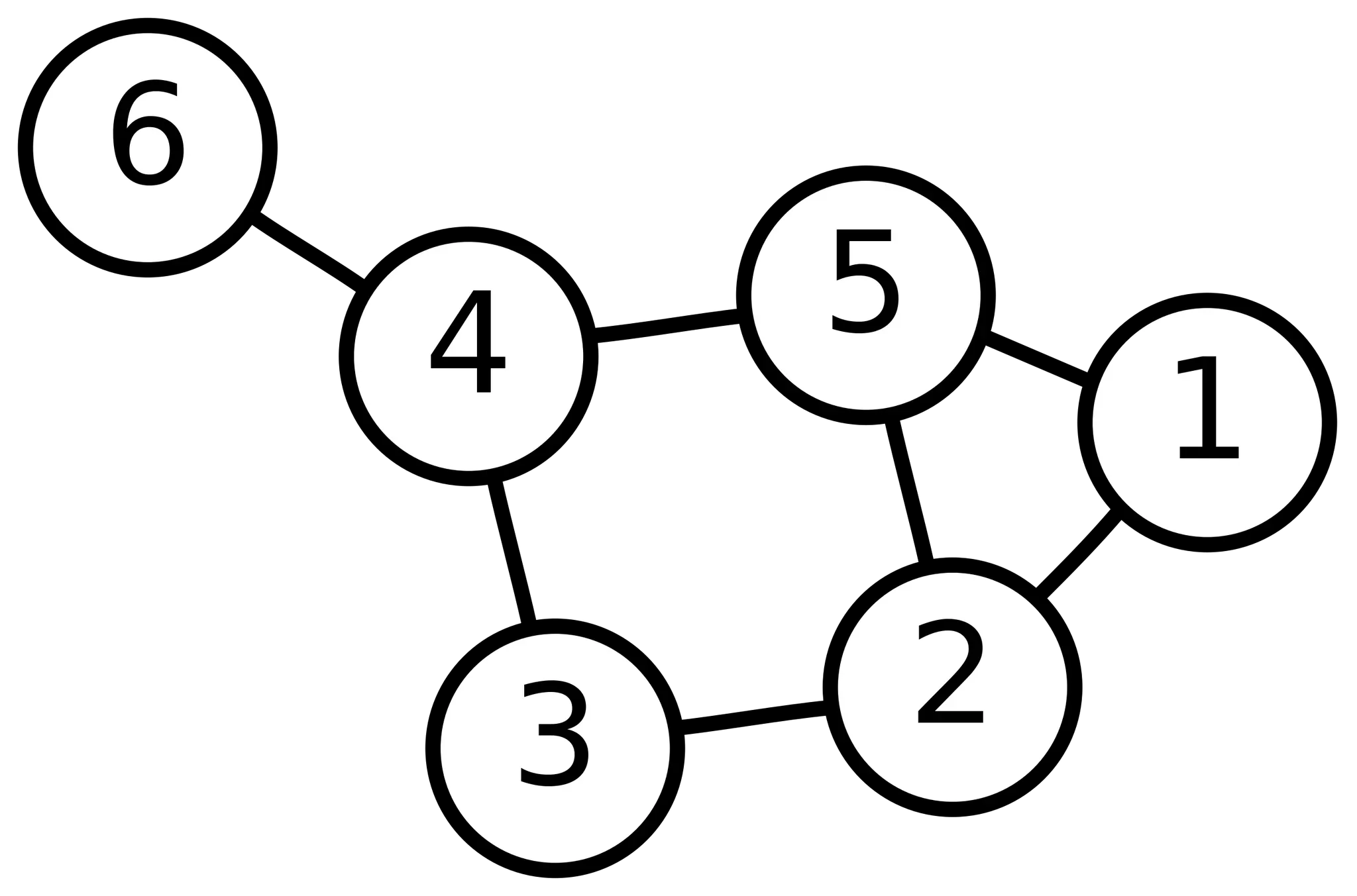
그래프 (Graph)는 정점(Vertex or Node)나 간선(Edge)로 구성되는 자료구조로, 객체 간의 관계를 표현한다. 방향성 여부에 따라 유향 그래프와 무향 그래프로 구분되며, 인접 리스트 또는 인접 행렬로 구현된다.
그래프 (Graph) 란?
그래프는 정점(vertex)과 간선(edge)으로 구성된 자료 구조로, 객체 간의 관계를 나타내는 데 사용된다. 다양한 문제에서 개체 간의 연결성을 표현하기 위해 사용되며, 정점은 개체를, 간선은 그 개체들 간의 관계를 의미한다.
•
정점 (Vertext / Node): 그래프를 구성하는 객체나 데이터.
•
간선 (Edge): 정점들을 잇는 선.
•
인접 (Adjacent): 간선으로 이어진 정점들의 관계를 “인접”하다라고 함.
그래프의 종류들
그래프는 여러 종류로 나뉘며, 각 종류는 그래프의 특성에 따라 다르게 정의된다.
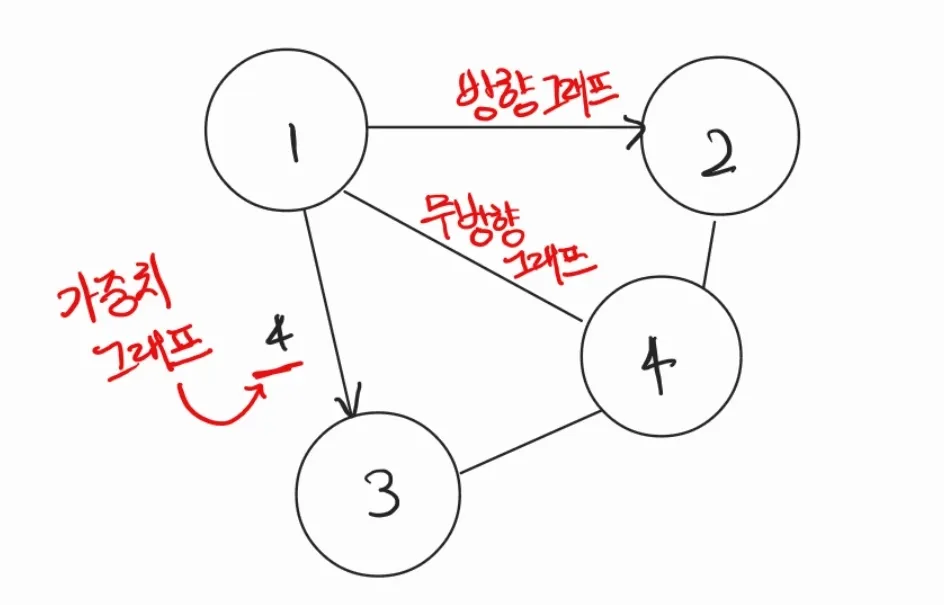
간선의 종류에 따라서 달라지는 그래프들을 한 번에 표시한 그림
•
가중치 그래프 (Weighted Graph)
가중치 그래프는 각 간선에 가중치가 할당된 그래프로, 간선의 가중치는 두 정점 사이의 연결에 대한 '비용'을 의미할 수 있다.
예를 들어, 도로 네트워크에서 각 도로의 길이를 가중치로 나타낼 수 있다.
•
무방향 그래프 (Undirected Graph)
무방향 그래프는 간선이 방향성을 갖지 않는 그래프이다. 즉, 간선이 두 정점을 연결할 때, 두 정점은 양방향으로 자유롭게 이동할 수 있다.
친구 관계 네트워크가 대표적인 예시이다.
•
방향 그래프 (Directed Graph)
방향 그래프는 간선에 방향성이 있는 그래프로, 한 정점에서 다른 정점으로 이동할 수 있는 방향이 정해져 있다.
예를 들어, 교통 네트워크에서 일방통행 도로를 나타낼 때 사용할 수 있다.
경로 (Path)
그래프 알고리즘에서 경로(Path)란 한 정점에서 시작하여 다른 정점으로 가는 연결된 간선들의 연속을 의미한다. 경로의 길이는 경로를 구성하는 간선의 개수로 측정되며, 경로가 순환하지 않는 경우 이를 단순 경로(Simple Path)라고 한다.
•
연결 그래프 (Connected Graph)
연결 그래프는 모든 정점들이 서로 연결된 그래프로, 어떤 정점에서 다른 정점으로 경로가 존재하는 그래프를 의미한다.
◦
절단 그래프 (Cut Graph)
특정 간선을 제거하면 그래프가 연결되지 않게 되는 그래프를 말한다. 이러한 간선을 절단 간선이라고 부른다.
◦
완전 그래프 (Complete Graph)
완전 그래프는 그래프의 모든 정점이 서로 간선으로 연결된 상태를 의미한다.
•
포리스트 (Forest)
포리스트는 트리(tree)의 집합을 의미하며, 그래프 내의 모든 연결 성분이 트리인 경우를 말한다. 즉, 순환이 없는 연결 그래프의 집합이다.
그래프 상에서 경로의 최단을 구하는 문제는 꽤나 중요한 문제이므로, 추후에 다룰 예정이다.
그래프 자료형들의 작업
그래프 자료구조에서 주로 수행되는 작업들은 다음과 같다.
•
Create: 그래프를 생성한다.
•
Destroy: 그래프를 삭제한다.
•
InsertVertex: 새로운 정점을 그래프에 추가한다.
•
InsertEdge: 두 정점을 연결하는 간선을 그래프에 추가한다.
•
DeleteVertex: 그래프에서 정점을 삭제한다.
•
RetrieveVertex: 그래프에서 특정 정점에 대한 정보를 조회한다.
•
IsAdjacent: 두 정점이 간선으로 연결되어 있는지 확인한다.
•
IsEmpty: 그래프가 비어 있는지 확인한다.
그래프 표현 방법
그래프를 표현하는 방법에는 주로 두 가지가 사용된다.
1.
인접행렬 (Adjacency Matrix)
인접행렬은 2차원 배열로 그래프를 표현하는 방식이다. 정점 간의 연결 여부를 행렬의 값으로 나타내며, 인접행렬의 크기는 그래프의 정점 수에 따라 결정된다. 이 방식은 정점 간 연결 여부를 빠르게 확인할 수 있지만, 메모리 사용량이 많다는 단점이 있다.
인접 행렬에서 인접하지 않은 노드를 표현하는 방법은 여러가지가 있다. 가는데 비용을 무한대로 둬서 엄청난 비용을 청구하기도 하며, 0으로 표현하기도 한다.
2.
인접 리스트 (Adjacency List)
인접 리스트는 각 정점에 연결된 다른 정점들의 리스트로 그래프를 표현하는 방식이다. 이 방식은 인접행렬보다 메모리 효율이 높으며, 특히 간선의 수가 적은 희소 그래프(sparse graph)에 적합하다. 그러나 간선 연결 여부를 확인하는 데는 시간이 더 많이 걸릴 수 있다.
그래프 구현 코드 (C++)
•
인접행렬로 구현
◦
동적 배열을 직접 만들어서 구현 (C)
▪
조금 어려운 길로 먼저 가보자.
▪
동적 배열을 만드는 방법은 이중 포인터를 기반으로 한다. 다만 동적 배열 역시 한 번 만들면 그 크기가 고정되므로 주의할 필요가 있다.
#include <stdio.h>
#include <stdlib.h>
//그래프 알고리즘
int** InitMatrix(int NRow, int NCol, int Value)
{
// Value는 Matrix 초기값
int **m;
m = malloc(NRow * sizeof(int *));
for (int i =0 ; i < NRow; i++) {
m[i] = malloc(NCol * sizeof(int));
}
for (int i = 0; i < NRow; i++) {
for (int j =0; j < NCol; j++) {
m[i][j] = Value;
}
}
return m;
}
void FreeMatrix(int **m, int NRow){
for (int i =0; i < NRow; i++) {
free(m[i]);
}
free(m);
}
typedef struct graphRecord{
int V;
int E;
int **M;
} graphType;
typedef graphType *graphPtr;
graphPtr InitGraph(int V) {
graphPtr G = malloc(sizeof(graphType));
G-> V = V;
G-> E = 0;
G-> M = InitMatrix(V, V, 0);
return G;
}
void InsertEdge(graphPtr g, int V1, int V2) {
if (g->M[V1][V2] == 0) {
g->E++;
g->M[V1][V2] = 1;
g->M[V2][V1] = 1;
}
}
void PrintMatrix(graphPtr g, int NRow) {
// Matrix
for (int i =0 ; i < NRow; i++) {
for (int j =0 ; j < NRow; j++) {
printf("%d ", g->M[i][j]);
}
printf("\n");
}
}
int main() {
graphPtr graph_1 = InitGraph(5);
InsertEdge(graph_1, 1, 0);
PrintMatrix(graph_1, 5);
}
C++
복사
▪
V 인 버텍스 수와, E 인 간선 수를 같이 나타내기 위해 구조체를 사용했다.
▪
하지만 알고리즘 문제를 풀 때, V와 E를 알아내고 따로 저장할 수 있다면…? 굳이 위에 방식처럼 할 필요는 없을 것이다.
◦
Vector 자료형으로 구현 (C++)
▪
Vector로 할지라도 클래스를 굳이 쓸 필요는 없다. 그냥 썼을 뿐…
▪
대부분의 알고리즘 문제풀이에서는 vector를 쓸 것이다. 동적 배열을 만드는 것을 굳이 할 필요가 없으니까 말이다.
#include <iostream>
#include <vector>
using namespace std;
class Graph {
private:
int numVertices;
vector<vector<int>> adjMatrix;
public:
Graph(int vertices) {
numVertices = vertices;
adjMatrix.resize(vertices, vector<int>(vertices, 0));
}
void insertEdge(int u, int v) {
adjMatrix[u][v] = 1;
adjMatrix[v][u] = 1; // 무방향 그래프인 경우
}
void displayMatrix() {
for (int i = 0; i < numVertices; i++) {
for (int j = 0; j < numVertices; j++) {
cout << adjMatrix[i][j] << " ";
}
cout << endl;
}
}
};
int main() {
Graph g(5);
g.insertEdge(0, 1);
g.insertEdge(0, 4);
g.insertEdge(1, 2);
g.insertEdge(1, 3);
g.insertEdge(1, 4);
g.displayMatrix();
return 0;
}
C++
복사
▪
다시 말하지만, 솔직히 class를 만들 필요는 없다. 어차피 인접행렬만 있으면 되고, 그래프에 담긴 데이터가 인덱스로 취급된다고 가정하면 vector<vector<int>> 로 만든 2차원 동적 배열만 있고 이걸로 처리하면 된다…
•
아래 코드로 쉽게 그래프를 만들 수 있다.
//인접 행렬 기반 구현
#include <vector>
#include <stdio.h>
using namespace std;
int main() {
int numNodes = 5;
//graph == adjacent Matrix;
// 인접 행렬을 0으로 초기화
vector<vector<int>> graph(numNodes + 1, vector<int>(numNodes + 1, 0));
// 노드 연결을 행렬에 반영 (양방향이 아니면 한쪽만 추가)
graph[1][2] = 1;
graph[1][3] = 1;
graph[2][4] = 1;
graph[3][5] = 1;
// 인접 행렬 출력
for (int i = 1; i <= numNodes; i++) {
for (int j = 1; j <= numNodes; j++) {
printf("%d ", graph[i][j]);
}
printf("\n");
}
return 0;
}
C++
복사
▪
다만 이 경우, 순회에서는 의도치 않은 작업이 일어날 수 있으므로 주의를 하긴 해야한다.
•
인접 리스트로 구현
#include <iostream>
#include <vector>
using namespace std;
class Graph {
private:
int numVertices;
vector<vector<int>> adjList;
public:
Graph(int vertices) {
numVertices = vertices;
adjList.resize(vertices);
}
void insertEdge(int u, int v) {
adjList[u].push_back(v);
adjList[v].push_back(u); // 무방향 그래프인 경우
}
void displayList() {
for (int i = 0; i < numVertices; i++) {
cout << "Vertex " << i << ":";
for (int j : adjList[i]) {
cout << " -> " << j;
}
cout << endl;
}
}
};
int main() {
Graph g(5);
g.insertEdge(0, 1);
g.insertEdge(0, 4);
g.insertEdge(1, 2);
g.insertEdge(1, 3);
g.insertEdge(1, 4);
g.displayList();
return 0;
}
C++
복사
•
마찬가지로, vector 자료형으로 쉽게 만들 수 있다.
// 인접 리스트 기반 구현
#include <vector>
#include <stdio.h>
using namespace std;
int main() {
int numNodes = 5;
vector<vector<int>> graph(numNodes); //첫 열과 첫 행은 무시.
graph[1] = {2, 3}; // 노드 번호대로 그대로 넣음
graph[2] = {4};
graph[3] = {5};
for (vector<int> vec: graph) {
for (int i = 0; i < vec.size(); i++) {
printf("%d ", vec[i]);
}
printf("\n");
}
} // 끝..
C++
복사
인접 행렬 vs 인접 리스트
DFS(깊이 우선 탐색) 등을 사용하여 그래프를 탐색할 때 그래프를 인접 행렬, 인접 리스트 중 어떤 걸 써서 구현했냐에 따라 성능 차이가 발생할 수 있다. 이는 추후 다시 다루도록 한다.
개인적으로는 인접 리스트 기반을 선호한다. 나는 인덱스 가지고 노는 것에 취약해서 최대한 인접 행렬의 인덱스 에러로 인한 결과 에러 위험이 없는 인접 리스트가 좋다.
요약
•
그래프는 정점과 간선으로 구성된 자료구조로, 다양한 종류의 그래프와 경로를 통해 객체 간의 관계를 나타낸다.
•
그래프는 인접행렬과 인접 리스트로 구현할 수 있으며, 각각의 장단점에 따라 사용된다.
궁금증
1.
왜 Vertex 자료형은 따로 선언하지 않는가?
•
잘 생각해보면 인접행렬에서 나타내는 인덱스들 (2차원 배열의 인덱스)은 사실상 노드의 고유 번호가 된다. 따라서, 고유 번호를 따라 Vertex가 담은 자료만 뽑아내면 되기 때문에 굳이 자료형을 만들어서 하지는 않았다.
REFERENCES
•
주우석, 2015, C/C++로 배우는 자료구조론, 한빛미디어
Written by Changyu Lee