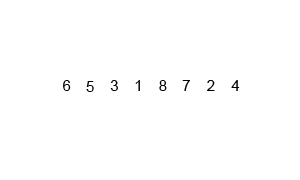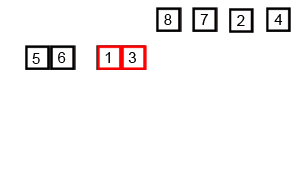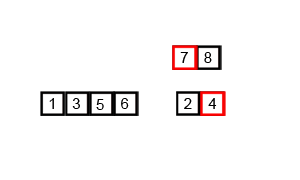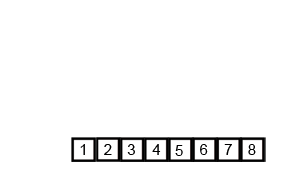Merge Sort (합병 정렬)
개요
합병 정렬 (Merge Sort)란 배열을 반으로 나누고 각각을 정렬한 후 합치는 분할 정복 알고리즘으로, 시간 복잡도는 O(n log n)입니다.
•
이름은 합병 정렬이다. 또는 병합 정렬이라고도 불린다. (밑에서 둘을 혼용함)
왜 “합병”인가?
합병 정렬은 기본적으로 재귀호출의 형태를 띈다. 재귀 호출을 하면서 배열을 반으로 분할시키고 이를 정렬한뒤 다시 합쳐서 정렬하는 반복 형태의 방식을 사용한다.
이 과정에서 분할하고, 정복한다는 분할-정복 (Divide and Conquer) 방식이 사용되며,
배열을 합친다는 개념 때문에 합병 (혹은 병학, Merge) 라는 이름이 붙은 알고리즘이다.
합병 정렬 작동 원리
아래는 합병정렬의 수도코드이다.
수도 코드조차 상당히 길지만 아래의 작동 원리를 살펴보면 이해할 수 있을 것이다.
function 합병정렬(배열):
if 배열의 길이 <= 1:
return 배열
중간 = 배열의 길이 / 2
왼쪽배열 = 합병정렬(배열[0:중간])
오른쪽배열 = 합병정렬(배열[중간:배열의 길이])
return 합병(왼쪽배열, 오른쪽배열)
function 합병(왼쪽배열, 오른쪽배열):
결과 = []
왼쪽인덱스 = 0
오른쪽인덱스 = 0
while 왼쪽인덱스 < 왼쪽배열의 길이 그리고 오른쪽인덱스 < 오른쪽배열의 길이:
if 왼쪽배열[왼쪽인덱스] < 오른쪽배열[오른쪽인덱스]:
결과.append(왼쪽배열[왼쪽인덱스])
왼쪽인덱스 += 1
else:
결과.append(오른쪽배열[오른쪽인덱스])
오른쪽인덱스 += 1
while 왼쪽인덱스 < 왼쪽배열의 길이:
결과.append(왼쪽배열[왼쪽인덱스])
왼쪽인덱스 += 1
while 오른쪽인덱스 < 오른쪽배열의 길이:
결과.append(오른쪽배열[오른쪽인덱스])
오른쪽인덱스 += 1
return 결과
C++
복사
예시를 살펴 보자.
합병 정렬은 배열 6, 5, 3, 1, 8, 7, 2, 4에서 다음과 같이 작동함.
1. 배열을 반으로 나눔
•
처음 배열을 반으로 나누면 두 개의 하위 배열이 생성됨.
◦
왼쪽: [6, 5, 3, 1]
◦
오른쪽: [8, 7, 2, 4]
2. 왼쪽 배열 [6, 5, 3, 1] 정렬
•
왼쪽 배열을 다시 반으로 나눔.
◦
왼쪽: [6, 5]
◦
오른쪽: [3, 1]
•
[6, 5]를 다시 나누면 [6]과 [5]로 나뉘고, 둘 다 하나의 요소이므로 바로 합침.
◦
합병: [5, 6]
•
[3, 1]도 [3]과 [1]로 나뉘고, 바로 합침.
◦
합병: [1, 3]
•
이제 두 배열 [5, 6]과 [1, 3]을 합침.
◦
합병: [1, 3, 5, 6]
3. 오른쪽 배열 [8, 7, 2, 4] 정렬
•
[8, 7]을 나누면 [8]과 [7]이 됨. 둘 다 바로 합침.
◦
합병: [7, 8]
•
[2, 4]도 [2]와 [4]로 나누고 바로 합침.
◦
합병: [2, 4]
•
이제 두 배열 [7, 8]과 [2, 4]를 합침.
◦
합병: [2, 4, 7, 8]
4. 최종 합병
•
마지막으로 왼쪽의 [1, 3, 5, 6]과 오른쪽의 [2, 4, 7, 8]을 합쳐 최종 배열 완성.
◦
합병: [1, 2, 3, 4, 5, 6, 7, 8]
이렇게 합병 정렬이 완료된다.
다시 수도 코드로 돌아와서, 자세히 설명을 해보자면.
합병 정렬은 크게 두 가지 단계로 이루어진다.
1.
분할(Divide): 배열을 더 이상 나눌 수 없을 때까지 반으로 나누는 단계
2.
정복(Conquer): 나눠진 배열을 차례로 합병하여 정렬하는 단계
즉, 배열을 최소 단위로 쪼갠 후, 다시 작은 배열들을 합쳐 나가며 정렬한다.
1. 합병 정렬의 메인 함수: 합병정렬(배열)
2. 배열을 합치는 함수: 합병(왼쪽배열, 오른쪽배열)
합병 정렬 코드 (C++)
#include <iostream>
#include <stdio.h>
// k는 정렬 횟수, num은 저장되는 수
int k;
int merge_count = 0;
int num;
int n;
void merge(int A[], int F, int Mid, int L) ;
void merge_sort(int A[], int First, int Last) {
if (First < Last) {
int Mid = (First + Last) / 2;
merge_sort(A, First, Mid);
merge_sort(A, Mid+1, Last);
merge(A, First, Mid, Last);
}
}
void merge(int A[], int F, int Mid, int L) {
int Temp[500000]; // 문제에서 주어진 MAX
int left_index = F;
int left_last_index = Mid;
int right_index = Mid +1;
int right_last_index = L;
int new_arr_index = F; //새로 저장할 배열의 시작 인덱스
// 어느 한 쪽이 안남을 때까지 반복
while ( (left_index <= left_last_index) && (right_index <= right_last_index) )
{
if (A[left_index] > A[right_index] ) {
Temp[new_arr_index] = A[right_index];
right_index++;
}
else {
Temp[new_arr_index] = A[left_index];
left_index++;
}
new_arr_index++;
}
//왼쪽이 남았을 때 처리
while (left_index <= left_last_index ) {
Temp[new_arr_index] = A[left_index];
left_index++;
new_arr_index++;
}
while (right_index <= right_last_index) {
Temp[new_arr_index] = A[right_index];
right_index++;
new_arr_index++;
}
// 임시 저장된 배열을 원래 배열로 복사
for (int i = F; i < new_arr_index; i++ ) {
num = Temp[i];
if (++merge_count == k) printf("%d", num);
A[i] = Temp[i];
}
}
int main() {
// 입력 받기
scanf("%d", &n);
scanf("%d", &k);
int* arr = new int[n];
for (int i =0 ; i < n; i++) {
scanf("%d", &arr[i]);
}
merge_sort(arr, 0, n-1);
if (k > merge_count) printf("-1");
}
C++
복사
합병 정렬의 시간 복잡도
위에서 살펴봤듯, 합병 정렬은 2가지 과정을 거친다. 분할과 정복이다.
따라서, 합병 정렬의 시간 복잡도를 계산하는 과정은, 합병 정렬의 분할과 합병 과정에서 소요되는 시간을 분석하는 방식으로 이루어진다.
•
1. 분할 과정 분석
합병 정렬은 배열을 반으로 나누는 분할(Divide) 과정과, 나누어진 배열을 다시 합치는 정복(Conquer) 과정으로 나뉨.
◦
배열을 분할하는 과정은 배열을 두 개의 하위 배열로 나누는 것이므로, 한 번 나눌 때 배열의 크기는 절반으로 줄어듦. 즉, 배열을 나눌 때마다 n -> n/2 -> n/4 -> ... 식으로 줄어들어, log n 단계에서 더 이상 나눌 수 없는 크기(배열의 길이가 1인 경우)가 됨.
따라서, 분할 과정은 한 번 배열을 나누는 데 O(1)의 시간이 소요되며, 배열을 완전히 나누는 데 log n 단계가 걸림.
•
2. 합병 과정 분석
나뉜 배열을 다시 합병하는 과정에서 소요되는 시간은 각 단계에서 배열의 모든 요소를 확인하며 합병하기 때문에, 배열의 크기만큼 시간이 걸림.
◦
각 단계에서 두 배열을 병합하는 데 걸리는 시간은 배열의 크기인 O(n)이 소요됨. 즉, 모든 요소를 한 번씩 비교하여 병합하는 과정이 필요하므로, **각 단계에서 O(n)**의 시간이 걸림.
•
3. 전체 시간 복잡도 계산
합병 정렬의 전체 시간 복잡도는 분할 단계와 각 분할된 배열을 병합하는 단계의 시간 복잡도를 결합하여 계산할 수 있음.
◦
분할 과정은 log n 단계에서 이루어지며, 각 단계에서 배열을 합병하는 데 O(n) 시간이 소요됨.
◦
따라서, 전체 시간 복잡도는 이 됨.
추가적으로,
합병 정렬은 쾌속 정렬과 비슷하게 Divide 와 Conquer 과정을 거친다.
그러나. 호출의 순서에 있어서 쾌속 정렬(Quick Sort)와는 정반대되는 것으로서, 쾌속 정렬과의 차이점에 유의해야한다.
합병 정렬은 배열을 쪼갠 후 정렬이므로 쪼개는 과정에서 입력 데이터 크기와 상관 없이 분할 과정의 시간 복잡도가 으로 고정된다. 또한, 기존의 순서를 보전하면서 정렬한다는 장점이 존재한다.
이는 피벗에 따라 알고리즘 효율이 달라지는 쾌속 정렬에 비해 안정적인 정렬로 불린다.
이는 쾌속 정렬을 하며 다시 공부해보자.
한편, 병합 정렬의 과정을 보면서 Temp는 배열을 봤을 것이다. 내가 직접 짠 알고리즘은 그냥 MAX를 때려박았지만… 최적화할라면 할 수 는 있을 것이다.
어찌됐건, Merge Sort는 기본적으로 추가적인 혹은 임시적인 저장 공간을 필요로한다. 이는 메모리를 추가로 사용하게 된다는 점에서 약점이 될 수는 있으나, 그래도 효율적인 알고리즘으로 평가되기에는 손색이 없을 것이다.
요약
•
합병 정렬은 배열을 반으로 나누고 각각을 정렬한 후 합치는 분할 정복 알고리즘으로, 시간 복잡도는 O(n log n)이다.
•
재귀적으로 배열을 나눈 뒤, 두 배열의 첫 요소부터 비교하여 작은 값을 선택하고, 남은 요소를 결과 배열에 추가하는 방식으로 작동한다.
•
합병 정렬은 배열을 나누어 처리하는 점에서 퀵 정렬과 비슷하지만, 합치는 과정이 있어 안정적인 정렬 알고리즘으로 평가된다.
관련 자료
•
REFERENCES
2.
주우석, 2015, C/C++로 배우는 자료구조론, 한빛미디어
Written by Changyu Lee